2024.09.22. 06:00
Magyar matematikusok értek el áttörést a biológiai formák geometriai leírásában
A HUN-REN és a BME által alapított Morfodinamika Kutatócsoport és az Oxfordi Egyetem matematikusai egy új, univerzális formaosztályt fedeztek fel.
A csonkolt oktaéder lágyított formája
Forrás: Regős Krisztina és Domokos Gábor
Ezek az úgynevezett lágy cellák a biológiai szövetek geometriai építőelemei, és számos helyen megtalálhatók a természetben, a csigáspolipoktól az izomsejtekig. Az eredmények nem csak a biológiai szövetek geometriáját magyarázhatják, hanem az építészeti tervezésben is új formavilágot teremthetnek. A rendkívüli felfedezésről a rangos PNAS Nexus folyóirat számolt be.
A matematikusokat Platón elmélete óta – amely az elemeket a szabályos poliéderekkel azonosította –foglalkoztatják a térkitöltő csempézések: azokat a formákat keresik, amelyek hézagok és átfedések nélkül borítják be a síkot vagy töltik ki a teret. A geometriában eddig leggyakrabban vizsgált térkitöltő formák (mint például a háromszögek, négyszögek a síkon, kockák és más poliéderek a térben) azonban éles csúcsokkal, egyenes élekkel és sík lapokkal rendelkeznek, ám ilyenek ritkán figyelhetőek meg élő szervezetekben.
Az evolúció rengeteg térkitöltő mintázatot hozott létre, például a biológiai szövetekben vagy a csigáspolipok cellás vázában. Ezek a mintázatok leginkább erősen ívelt élekkel, görbült felületekkel és kevés, esetenként nulla éles sarokkal rendelkező formákból épülnek fel.
Eddig rejtély volt, hogy a természetben miként fejlődnek ki ezek a geometriailag összetett „lágy alakzatok”.
A választ Domokos Gábor, Regős Krisztina és G. Horváth Ákos (HUN-REN-BME Morfodinamika Kutatócsoport és Budapesti Műszaki és Gazdaságtudományi Egyetem) valamint Alain Goriely (Oxfordi Egyetem) adta meg a PNAS Nexus tudományos folyóiratban most megjelent cikkükben, amelyben ezeket a lágy cellákat mint a matematikai formák egy új osztályát írják le.
Ha két dimenzióban nézzük, a lágy celláknak görbe éleik vannak és mindössze két csúcsuk. Ilyen minták láthatók például az izomsejtekben, a zebra csíkjaiban, a folyami szigetek alakjában, a hagymarétegekben és még az építészeti tervezésben is.
Három dimenzióban a szóban forgó alakzatok összetettebbé és még érdekesebbé válnak: A kutatók először megállapították, hogy a térbeli lágy celláknak egyáltalán nincs csúcsuk. Majd egy olyan eljárást adtak meg, mely egy ismert poliéderes (éles) mintázatból (mint például a kockarács) kiindulva az élek megfelelő deformálásával egy lágy cellákból álló térkitöltést hoz létre. Ezen eljárás alkalmazása során több lágy cellatípust is azonosítottak.
Nem sokkal később a lágy formáknak számos példájára lettek figyelmesek a természetes és épített környezetben. A legmegdöbbentőbb felfedezésük az volt, hogy az ikonikus Nautilus csigáspolip belső kamrái maguk is lágy cellák.
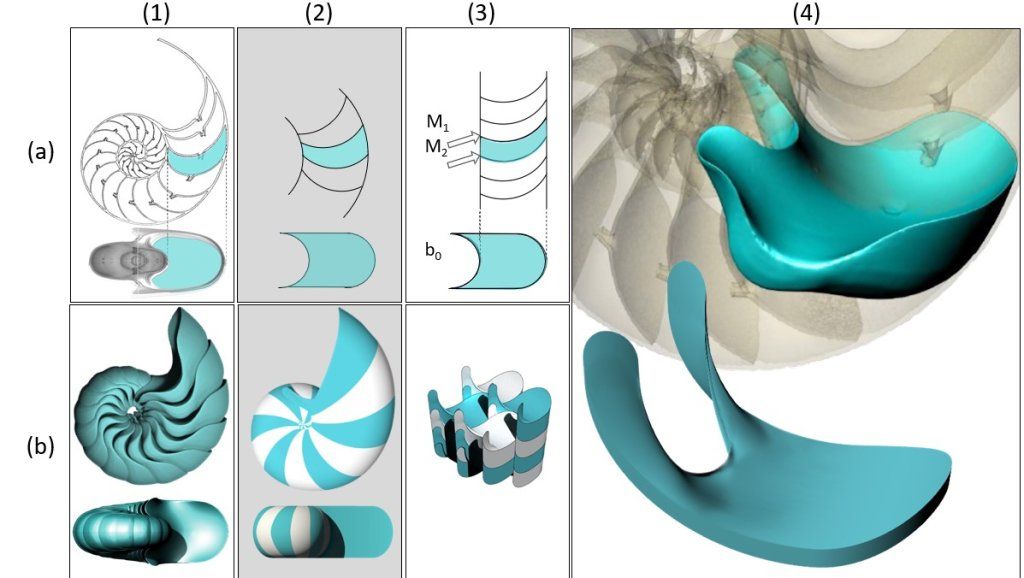
Forrás: Czeglédi Lajos és Regős Krisztina
Annak ellenére, hogy a kamráknak síkban két csúcsuk van, az a sejtésem támadt, hogy három dimenzióban nem lesznek csúcsok
– mondta Regős Krisztina, a kutatócsoport munkatársa. Részletes CT-felvételek segítségével a csapat aztán valóban megállapította, hogy a Nautilus és számos ammonites kamrái lágy cellák, amelyek sarkok nélkül töltik ki a külső vázat.
Domokos Gábor elmondta: „Azt láttuk, hogy az építészek – köztük Zaha Hadid (2016-ban elhunyt, világhírű iraki építész) – amikor el akarták kerülni a sarkokat, ösztönösen a lágy formákhoz nyúltak. Egy fiatal építészcsapatot pedig a Gömböc formája inspirálta arra, hogy megalkosson egy térbeli lágy cellát.”
Úgy tűnik tehát, hogy a lágy cellák a biológiai szövetek geometriai építőelemei, és létezésük számos érdekes kérdést vet fel a geometria és a biológia területén: a lágy csempézések létezésére vonatkozó szükséges geometriai feltételek új megvilágításba helyezhetik, miért részesít előnyben a természet bizonyos mintázatokat. A lágy cellák koncepciója segíthet megmagyarázni nemcsak a szövetek statikus geometriáját, hanem a növények gyökereinek növekedését is, amely az egyik legelterjedtebb biológiai formafejlődési folyamat.
Digitália
- Hologram segítségével keresik a magyar szexmunkásnő gyilkosát (videó)
- Saját halálos mellrákját kezelte (sikeresen) egy tudós vírusterápiával
- A világ legkelendőbb telefonja: kitalálja, melyik az?
- Hazai tervezésű pilóta nélküli légijármű forradalmasítja a tisztítástechnológiát
- Ezért van mesterséges intelligencia a Samsung tévéiben












